S530
小角X線散乱による架橋構造の動径分布解析
試料が希薄な場合、散乱強度は各粒子からの散乱強度の和として表されるが、粒子の濃度が高い場合や凝集している場合など、粒子間の干渉効果が無視できないとき、散乱強度I(q)は粒子の形状に起因する形状因子(Form Factor)F(q)と、粒子の配置に起因する構造因子(Structure Factor)S(q)とに分けて考えることになる。さらに、粒子が単分散で等方的であると仮定すると、I(q)はF(q)とS(q)の積に比例することが知られている*1。
I(q)∝ F(q)S(q)
このS(q)は動径分布関数g(r)とフーリエ変換の関係にあり*2、S(q)を抽出・変換すると、g(r)の様相から試料の構造を評価することが可能となる。
市販ゴム製品で実験したSAXS散乱強度を図1に示す。劣化により散乱強度の特有な変化を確認できる。
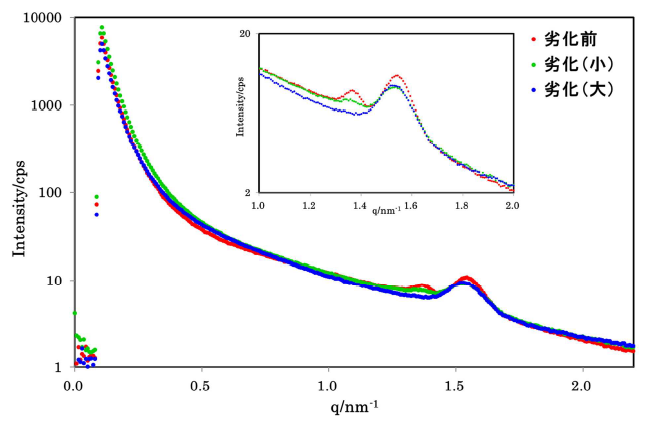
図1:ゴム製品のSAXS散乱強度
次に散乱強度のS(q)をフーリエ変換して得られる動径分布関数g(r)を図2に示す。劣化により架橋構造とその構造相関に生じた変化を捉えている。

図2:劣化前後ゴム製品の動径分布関数
さらに、伸張した状態のまま測定したSAXS散乱強度から動径分布関数図3を求めた。劣化により生じた新たな構造相関は、引張によって消失している。これは新たな構造の相関距離が一定に保たれなくなった様相が推測される。

図3:引張有無ゴム製品の動径分布関数
- *1 雨宮慶幸、篠原佑也、日本放射光学会誌、19、338(2006)
- *2 松岡秀樹、日本結晶学会誌、41、213(1999)