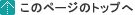元素偏在の定量的評価の試み
−ジニ係数−

元素マッピングの結果から「元素の均質に分布しているか否か、試料間で比較したい」という要望があります。貧富の偏りを表す指標として知られるジニ係数を使ってEPMA測定マップの定量的評価を試みたので、紹介します。

テストデータはテスト試料の測定結果で、

を用いて解析してみました。

図1がマップですが、画像として均質性を比較するだけですので、測定範囲や、画素数が異なっても最終的に規格化しますので、そろえる必要はありません。

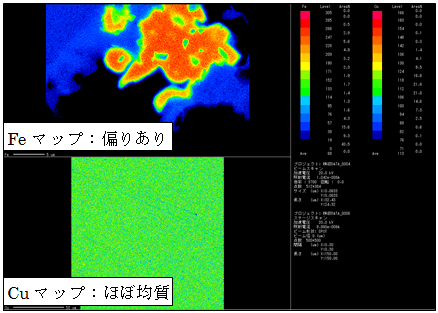
図1：テストに使ったEPMAマップ（Fe、Cu）

ジニ係数によるマップ解析では、各画素（500×500点であれば25万画素）の強度を使います。各点を強度の順に並べ、同時にその順位までの総和を計算します。各点の強度が等しい均質なマップであれば、順位1位から最後までリニアに総和が推移しますが、不均一であれば、順位の終盤に急激に総和が増加します。この様子を規格化したうえでグラフ化したのが図2で、ローレンツ曲線と呼ばれます。規格化しているため、画素数や平均強度の異なるマップでも同一のグラフ上で比較することが可能です。均質なマップでは、原点から対角の（1，1）に直線的なグラフとなり、不均質なマップになるほどグラフが下側に膨らんだカーブとなります。

グラフ上で、原点（0，0）から対角（1，1）を結ぶ対角線とローレンツ曲線が囲む面積の2倍がジニ係数で、均質な状態からの乖離を評価する指標となります。完全に均質であれば、面積0でジニ係数0、完全な不均一（1画素のみ大きなカウントで、他は0カウントの状態）であれば面積0.5でジニ係数は1になります。実際のマップでは、均質なCuマップで0.05、分布のあるFeマップで0.63でした。

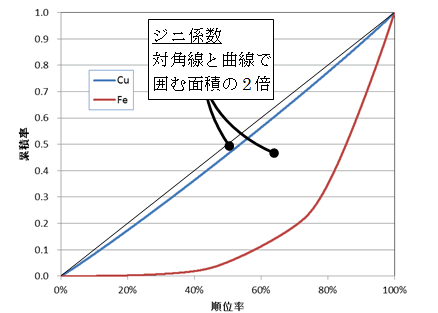
図2：マップのローレンツ曲線の比較

分散性の評価にはさまざまな手法がありますが、ここで示したようにジニ係数によっても評価できることが判りました。