JKR理論を用いた低弾性率粘着層の弾性率と界面エネルギー評価
(ナノインデンテーション)
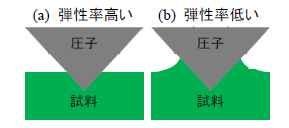
図1:圧子と試料の相互作用概念図
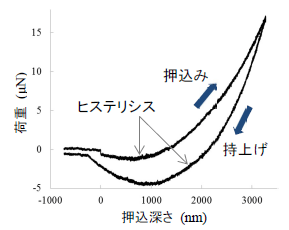
図2:スマホ用粘着層の荷重変位曲線
ナノインデンテーション試験は微小領域の複合弾性率や硬さを求めることができる。この時、Oliver-Pharr*1 の解析方法が一般的に適用される。この解析方法は弾性率が高い場合(数10MPa以上)に適用される(図1(a))。すなわち、弾性変形の機械的エネルギーが界面エネルギーより遥かに大きいことが前提となるため、凝着力による試料の変形は無視される。
一方、弾性率が低い場合(数MPa以下)、凝着力による試料の変形が顕著となる(図1(b))。図2はスマホ用粘着層(シリコンエラストマー)の荷重変位曲線である(技術資料P316参照)。凝着力が大きいため、持上げ曲線が押込み曲線と大きく異なるヒステリシスを示す。特に持上げにおいて荷重が大きくマイナス側に振れているのは、凝着力により見かけ上圧子が引っ張られているためである。この様な試料では一般的なOliver-Pharrの解析方法の適用には限界がある。このため、持上げ時の接線の傾きから求めた複合弾性率(1.6〜1.7MPa)は参考値と考えるべきである。
凝着力が含まれる接触理論として、熱力学を用いたJKR*2 接触理論が開発された。ここでは、放物体の圧子と凝着力のある弾性固体の接触の荷重と変位の関数が示された。このJKR理論は現在もAFM分野などで広く利用されている。JKR理論は球体を近づく放物体圧子を仮定するが、ナノインデンテーションに使われるバーコビッチなどは先端が丸まった円錐である。Sun*3 らは双曲体圧子を仮定しJKR接触理論を発展させた。Sun-JKR理論用いて図2の荷重変位曲線を計算し*4、得られた弾性率と界面エネルギーを表1にまとめた。押込みと持上げで界面エネルギーが大きく異なる。これは、粘着層を引き離す時の実効的な界面エネルギーが大きいことを示している。
| モード | 弾性率 | 界面エネルギー |
|---|---|---|
| 押込み | 0.83±0.02 MPa | 0.042±0.001 J/m2 |
| 持上げ | 1.14±0.01 MPa | 0.088±0.001 J/m2 |
*1 W. C. Oliver and G.M. Pharr, J. Mat. Res., 7, 1564 (1992)
*2 K. L. Johnson, K. Kendall and A. D. Roberts, Proc, R. Soc. London, Ser. A 324, 301 (1971)
*3 Y. Sun, B. Akhremitchev and G. C. Walker, Lang., 20, 5837 (2004)
*4 P-h 曲線解析ソフト "Modulus Fit"