流体シミュレーションに基づく多孔質材料の細孔構造解析

STEMトモグラフィなどによって試料の三次元構造が得られれば、その特徴を数値化できます。以下では、多孔質材料の細孔構造を解析した事例を紹介します。

STEMトモグラフィによって、多孔質カーボンの三次元再構成像を取得し、セグメンテーション（領域分割）しました（図1（a））。ここでは、その一部（関心領域, 図1（b））を選択して説明します。関心領域のうち、カーボン以外を細孔とみなし、細孔に流体が流れるものとして、シミュレーションしました。

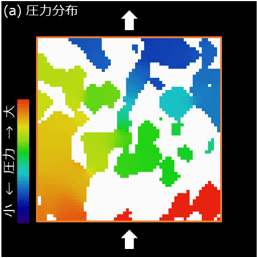
流れ方向を+ y方向とし、流体条件（出入口圧力, 流体粘度）を指定した場合の流体シミュレーション結果を図2に示します。ここでは、三次元分布を特定の平面で切り出した二次元分布を示しています。出口に向かって圧力が減少する傾向や、くびれや細孔端部で流速が小さい傾向が見られます。

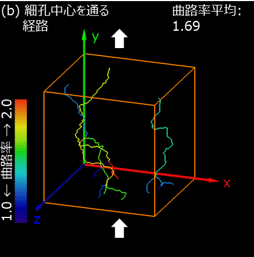
細孔領域に多数のマーカーを存在させた場合、図2の分布に応じて、多数の経路を描くことができます（図3（a））。ここでは、太い細孔ほど多くの経路が通過することや、細孔端部付近を通る経路も存在することが確認でき、流体流れの特徴を反映していると考えられます。これらは、細孔中心を通る経路（図3（b））には見られない特徴です。

経路は、曲路率という指標で数値化できます（技術資料「STEMトモグラフィによる多孔質アルミナの細孔解析（2）」参照）。曲路率は迂回の程度を表し、経路に沿った迂回距離fと、経路端点間の直線距離sの比で定義されます（曲路率τ = f / s）。三次元の関心領域について経路と曲路率を図4に示します。

以上のように、流体流れの特徴に基づいた上で、細孔構造を解析できます。