P312
微小領域の複合弾性率および硬さ評価(ナノインデンテーション)
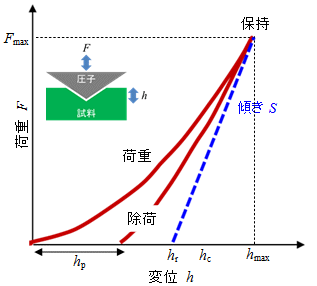
図1:荷重変位曲線概念図
図1に荷重変位曲線を示す。圧子を試料に押込み最大荷重(Fmax)に到達後、最大荷重で一定時間保持する。その後、荷重ゼロまで除荷して元に戻す。このため荷重変位曲線は3つの領域、すなわち荷重、保持、除荷領域から構成される。
荷重変位曲線を解析することにより、以下のパラメーターが得られる。
すなわち、
| S | : | 除荷曲線の最大荷重における接線の傾き |
| hp | : | 除荷曲線と横軸(変位)との交点(塑性変形量) |
| hr | : | 接線と横軸(変位)との交点 |
試料と圧子の接触面積は荷重変位曲線の解析値に大きく影響するため、接触深さ(hc)を正確に求めなければならない。hcは式(1)より求められる。ここで、εは圧子の形状で決まり、例えばバーコビッチの場合0.75が採用されている。
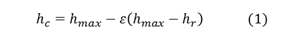

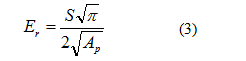
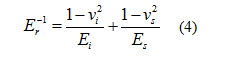
v:ポアソン比、i:圧子、s: 試料
硬さ(H)と複合弾性率(Er)はそれぞれ式(2)と(3)より求める*1。ここで、Apとは圧子の接触投影面積であり、接触深さ(hc)より求まる。式(4)より、ナノインデンテーション試験より得られる複合弾性率(Er)を一般的なヤング率と比較するためには、試料のポアソン比(vs)と圧子のポアソン比(vi)およびヤング率(Ei)が必要である。
図2に溶融石英、エポキシ、ポリエチレン(HD)の典型的な荷重変位曲線を示し、算出した複合弾性率と硬さも併せて示した。
*1 W. C. Oliver and G.M. Pharr, J. Mat. Res., 7, 1564 (1992)
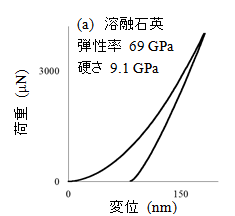
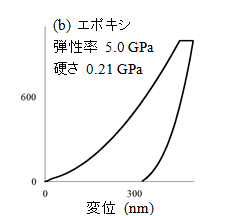
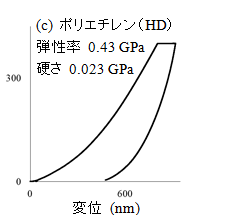
図2:荷重変位曲線から複合弾性率と硬さの解析