電子線動径分布解析法によるAuナノ粒子の構造解析

動径分布関数は、任意の原子の周りの原子の分布を示した関数です。実験的に動径分布関数を求めるためには、X線や電子線、中性子線の散乱現象を利用する必要がありますが、電子線の場合、TEMの拡大機能を用いることで高空間分解能での解析が可能です。今回は、Mitchellらの手法*1で電子線動径分布解析を行った事例をご紹介します。

電子回折パターンからの回折強度の抽出

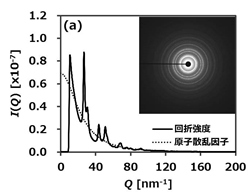
Auナノ粒子の電子回折パターンを図1（a） に示します。この回折強度を動径方向に積算し、波数Qに対してプロットした回折強度
I(Q)を同図 に示します。ここで、波数：Q = (4πsinθ) / λ = 2π / d, 回折角：2θ, 電子線の波長：λ, 逆空間上の距離：1/d です。

還元干渉関数の導出

Auの原子散乱因子（文献値）を図1（a）に示します。これをN倍しI(Q)に近づくようにフィッティングします。フィッティング後の両者の差分に相当するものが還元干渉関数F(Q)です。

2体分布関数の導出

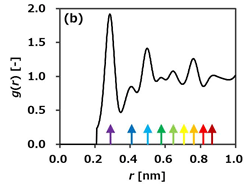
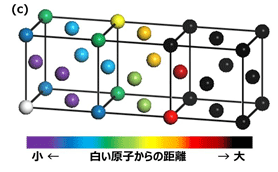
F(Q)をフーリエ変換すると、2体分布関数g(r)が得られます（図1（b））。ここでg(r)は、任意の原子から距離rだけ離れた位置に他の原子を見出す確率を表します。図1（b）では、Au（fcc）の結晶構造（図1（c））から求めた原子間距離を矢印で示しており、矢印の色は結晶構造の原子の色と対応しています。ここから、g(r)のピーク位置と矢印の位置が比較的良く対応しており、秩序構造を有していることが確認できます。

動径分布関数の導出

試料の平均原子数密度をρ₀とすると、動径分布関数は4πr²ρ₀g(r)で与えられます（図1（d））。これは、任意の原子から距離rとr + drの球殻中に存在する原子の数密度を表します。動径分布関数の第一ピークの面積から平均の配位数を求めることもできます。なお、今回は触れませんが、非晶質材料についても同様に解析可能です。

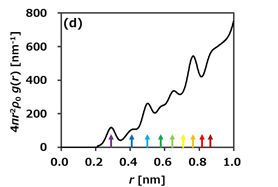図1：（a）Auナノ粒子の電子回折パターン、回折強度I(Q)、原子散乱因子、（b）2体分布関数g(r)、
（c）Au（fcc）の結晶構造、（d）動径分布関数4πr²ρ₀g(r)

*1 D. R. G. Mitchell and T. Petersen, Microsc. Res. Tech., 75(2), 153-163, 2012.